토목구조기술사 121-2-5
- 토목구조기술사
- 2020. 5. 28.

풀이) ※ 틀린부분은 취소선과 빨간색으로 처리함_20-12-31
1> 부재 접합부 늘음량(변형률)을 구한다.
1번 부재가 늘어나는 형상을 다음과 같이 나타낼 수 있다. 2번 부재가 저항하여 1번 부재에 압축력이 생기고 모멘트가 작용한다. 2번 부재도 같은 축력으로 인장력이 발생하고 모멘트가 작용한다.

1. 부재별 모멘트 산정
모멘트 평형 식 ①에 부재 휨 곡률식 ②를 대입하여 구한다.

2. 축력산정
변형률 조건식 ③에 접합부 부재별 응력 ④를 대입하여 축력을 구한다.

3. 값 대입으로 축력 산정

4. 값 대입으로 모멘트와 응력 산정

5. 값 대입으로 변형률 산정

2> B점 반력 산정
접합부 원의 반지름을 R₁ 라 하고 2번 부재 하단의 원 반지름을 R이라 한다. 부채꼴이 이루는 각도는 θ, B점에서 변형량을 d라 한다.

1>에서 구한 변형률과 곡률 조건으로 각도를 구한다.

변형량 d를 구한다.

2번부재 원의 반지름을 R₁이라 하고 하단의 원 반지름을 R이라 한다. B점에서 변형량을 d라한다.

휨곡률 관계에서 R을 구한다.

부채꼴이 이루는 각도 θ는 단부 변형률과 2번 부재 높이로 구하고 이를 이용해 d를 구한다.

B 점에 반력(P라 가정)이 작용하여 변형량 d만큼 처짐이 발생했다고 볼 수 있다.
탄성계수비 n=50/20=2.5 를 2번 부재의 폭에 곱하여 합성보 제계수를 구한다.

A = 200x100+500x200=120000mm²
yn=(200x100x250+500x200x100)/(200x100+500x200)=125mm
I₁=(200x100^3)/12+(200x100)x(50+(200-125))^2=329166666.667mm^4
I₂=(500x200^3)/12+(500x200)x(125-100)^2=395833333.333mm^4
I₁+I₂=725000000mm^4
d는 단순보 중앙에 집중하중 발생시 처짐과 같고 P(B점 반력)를 구한다.
d=PL³/48E₁I
→ P = 48E₁Id/L³=48x20x725000000x18.992/8000³=25.817N
→ P = 48E₁Id/L³=48x20x725000000x137.197/8000³=186.5 N
참고
기존 틀린 풀이)
B점이 없다고 보고 1번 부재에 온도가 증가했을 때 형상은 아래와 같다.
1번, 2번 부재가 이루는 원의 반지름을 각각 R₁, R₂ 라 하고 2번 부재 하단의 원 반지름을 R이라 한다. 부채꼴이 이루는 각도는 θ, B점에서 변형량을 d라 한다.

휘어진 두 부재의 길이 차는 1번 부재의 온도에 의한 늘음량과 동일하다.(L은 전체 길이 8m)
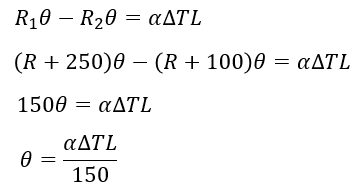
αΔTL=10x10^(-5)x50x8000=40mm
θ=αΔTL/150=40/150=0.266667rad(15.27887deg)

R₁=(8000+40)/0.26667=30150mm
R=30150-250=29900mm
d=29900-29900xcos(15.27887/2)=265.384mm
B 점에 반력(P라 가정)이 작용하여 변형량 d만큼 처짐이 발생했다고 볼 수 있다.
탄성계수비 n=50/20=2.5 를 2번 부재의 폭에 곱하여 합성보 제계수를 구한다.

A = 200x100+500x200=120000mm²
yn=(200x100x250+500x200x100)/(200x100+500x200)=125mm
I₁=(200x100^3)/12+(200x100)x(50+(200-125))^2=329166666.667mm^4
I₂=(500x200^3)/12+(500x200)x(125-100)^2=395833333.333mm^4
I₁+I₂=725000000mm^4
d는 단순보 중앙에 집중하중 발생시 처짐과 같고 P(B점 반력)를 구한다.
d=PL³/48E₁I
→ P = 48E₁Id/L³=48x20x725000000x265.384/8000³=360.757N
※ 위 풀이를 보고 답글을 주신 분이 있습니다. 1번 부재가 늘어나면서 2번 부재에 영향을 미치니 1번 부재 늘음량이 8040mm은 아닐 거라고 합니다. 맞는 말씀해 주셨습니다. 그런데 어떻게 식을 세워야 할 지 떠오르질 않아서 우선은 놔두고 있습니다...위 풀이는 틀린 것 같으니 참조만 해주시기 바랍니다.
'토목구조기술사' 카테고리의 다른 글
| 토목구조기술사 122-3-5 (0) | 2020.11.30 |
|---|---|
| 토목구조기술사 122-4-6 (0) | 2020.11.26 |
| 토목구조기술사 121-3-6 (0) | 2020.05.25 |
| 토목구조기술사 121-1-13 (0) | 2020.05.23 |
| 토목구조기술사 121-1-11 (0) | 2020.05.18 |