링(Ring) 상하 집중하중에 대한 처짐2
- Structural
- 2023. 11. 20.
지난 포스팅에서 링구조 상하 집중하중 P가 발생할 때 생기는 수직처짐을 구했습니다.
https://kkaesaem.tistory.com/348
링(Ring) 상하 집중하중에 대한 처짐
링구조 상하에 P 집중하중이 작용할 때 P점에 생기는 수직처짐을 구해보겠습니다. 문제) EI가 일정한 링, P 집중하중에 의한 수직변위는? 풀이) - 축력 및 전단에 의한 처짐은 무시 대칭 구조이므
kkaesaem.tistory.com
이번에는 똑같은 상황에서 수평처짐을 구해보겠습니다.

문제) EI가 일정한 링, 상하 집중하중 P에 의한 측 수평변위는?

풀이)
-축력 및 전단에 의한 처짐은 무시
대칭 구조, 원형 상단 절반 구조로 본다. 양 끝점에 P/2 만큼 반대방향 힘이 작용, 양 끝점 사이를 좁아지게 하는 모멘트 M(미지수)를 가정한다

최소일의 원리에 의해 미지수 M을 풀고, M_θ 산정.
(대칭구조를 이용해 0~π/2 구간 적분 x 2)

측 수평변위를 구하기 위해 측면에 단위하중 1 재하

절반구조로 보았을 때 양측에 1의 절반인 1/2 수평력과 모멘트 m(미지수)이 작용

m은 위에서 구한 M_θ에서 P=1, θ=π/2를 대입하면 구할 수 있다.
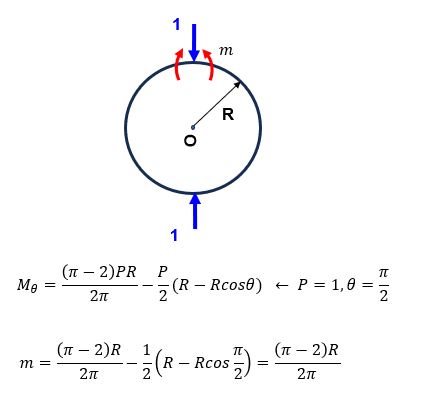
단위 하중법에 의해 측 수평변위 산정.
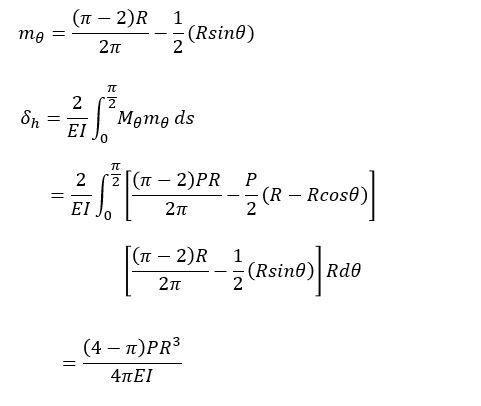
'Structural' 카테고리의 다른 글
| 중공원형(Pipe)단면 소성계수 (0) | 2024.03.24 |
|---|---|
| 반원 단면1차, 단면 2차 모멘트 및 도심 구하기 (0) | 2023.11.22 |
| 링(Ring) 상하 집중하중에 대한 처짐 (0) | 2023.11.19 |
| 고정단보 중앙 모멘트 작용시 문제 (0) | 2023.11.17 |
| 고정단보 집중하중 [Fixed Beam Concentrated load] (0) | 2023.11.05 |