Math] 원 위에서 움직이는(회전 혹은 구르는) 점의 변화 값 산정

원 위에서 움직이는 한 점의 변화(회전 혹은 구르는) 값을 산정해 보겠습니다. 아래와 같이 반경 R인 원 위의 접점에서 수직높이가 h인 A가 있습니다. 원 중심이 (0,0)이면 A점은 (0, R+h)가 됩니다.

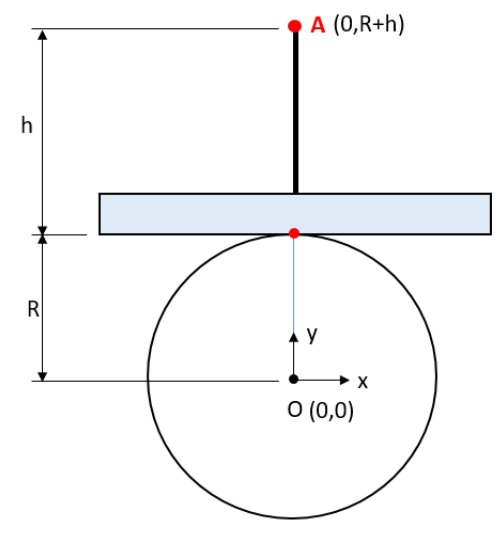
접점에서 회전하느냐 혹은 굴러가느냐에 따라 A의 변화 값은 다릅니다. 각각을 살펴보겠습니다.

 

1. 회전일 경우

α 만큼 회전했다고 하면 삼각함수 공식으로 Δx1과 Δy1를 구할 수 있습니다.

 

 

A1 의 좌표는 원의 중심이 0,0이므로 다음과 같이 됩니다.

 

 

2. 굴렀을 경우

접점이 뜨면서 α 각도로 기울어지게 굴렀다고 볼 수 있습니다. 순서를 나누어서 보면 더 쉽게 계산이 가능합니다.

α 각도로 회전 후, 호의 길이(αR)만큼 평행이동 하면 됩니다. 평행이동 점을 확대해 보면 α가 한 각인 직각삼각형이므로  Δx2과 Δy2를 구해보겠습니다.

 

A2 의 좌표는 다음과 같습니다.